
PYTHAGOREAN, Van ZWOLLE,
MEANTONE, SILBERMANN,
RAMEAU, WERKMEISTER,
KIRNBERGER,
ITALIAN 18th CENTURY Scales
Harpsichord
and
Pipe Organ Samples

|
PYTHAGOREAN, Van ZWOLLE,
Harpsichord |
Now you can explore these important historical temperaments on your ENSONIQ MIRAGE by simple parameter changes. This disk provides fourteen different scales in all twelve keys plus two full octaves of transposition. Play RENAISSANCE and BAROQUE pieces in the temperament in which they were written. Explore temperament in modern literature with modern instruments. Works with all MIRAGE compatible sound disks
A new version of ENSONIQ's 3.2 operating system by Dick Lord, UPWARD CONCEPTS
This disk contains a modified version of Ensoniq's OS 3.2 for the MIRAGE. If you start your MIRAGE with this disk in place (or you restart your MIRAGE by loading "UPPER", "LOWER", "0", "START") you will be able to explore the world of alternate temperaments.
Each of the 14 temperaments on this disk is a subtle change in the way the notes within each octave are tuned. If the idea of temperament is new to you, you may wish to try two different experiments. First, call up parameter 74 which should be 00 for an equal-tempered scale. Play a C-E-G chord and notice that the notes beat against each other. Step parameter 74 to 03 and play the C-E-G chord again. The chord will be pure. You are listening to a MEANTONE scale. Certain chords sound better than they do in equal temperament, but other intervals are impure. Leave parameter 74 at 03 (MEANTONE) and load sequence #1 from the disk. Play the sequence and notice how pure it sounds. This MEANTONE scale is based on C. Now change the value of parameter 73 from 00 to 01. The scale is now based on C#. Play the sequence again and notice how sour the pitches seem to be.
An equal-tempered scale sounds the same in any key, but the other scales on this disk do not.. A non-equal temperament must be based on a key that is harmonious with the key in which a piece of music is played or else dissonance will result.
The HARPSICHORD sample on this disk was sampled directly from the eight ft. stop of a William Post Ross one-manual harpsichord. The ORGAN samples were from a Reiger tracker-action pipe organ. Individual notes of this organ were digitally recorded by a SONY PCM-501ES encoder and VHS video recorder. The five sequences are excerpts from J, S. Bach: Brandenburg #3, Invention #13, Invention #8, Fugue in C Minor, and Freu'dich sehr, o meine Seele.
Sampling has been disabled on this disk to make room for the temperament
parameters and software. For sampling, use a normal OS 3.2 disk
instead of this TEMPERAMENT disk. You can use the TEMPERAMENT
disk with any MIRAGE sound sample or sequence. Once the operating
system on the TEMPERAMENT disk has been loaded, you can load other
sounds and sequences and then play them in any of the fourteen
scales available with the TEMPERAMENT operating system on this
disk.
Multi-TEMPERED Scales
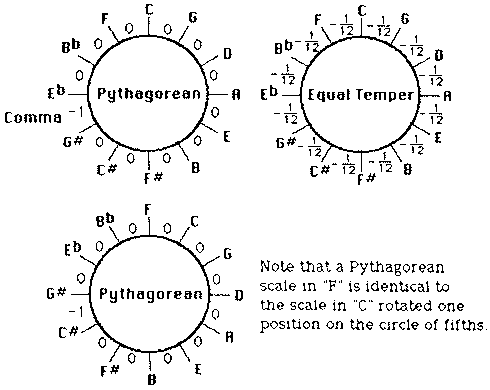
Experimentation with temperament has a very long history. Pythagorus (500 BC) made note of the difficulty of tuning instruments to a perfect scale. If you play a note and then sound another note that is a pure fifth above it, the pitches will have a ratio of 3:2. If you keep raising the pitch by a fifth (dropping back an octave whenever necessary to stay in the same area of the keyboard) you will make a circle that ends on a pitch just slightly above the note that you started on. You will not come out exactly on the original pitch. The error is the ratio (3/2) raised to the twelfth power and divided by 128, or approximately 1.0136:1, and this error is known as the Pythagorean Comma. The history of temperament is the story of how various music theorists have attempted to distribute the Comma throughout the octave. Pythagorus simply left the entire Comma between G# and Eb. Many others tried for sweeter fourths and thirds. Many scales have their own unique character. All suffer when transposed to different pitches. In the 18th century, the ability to transpose became so important that equal subdivision of the Comma was accepted, leaving all intervals impure. Today the equal-tempered scale is so common that few modern instruments can play any other scale. With your MIRAGE, you can explore all these temperaments by changing a parameter value.
73 Key
|
74 Temperament
|
76 Transpose
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| To play a MEANTONE scale in the key of F, set parameter 73 to 05 and parameter 74 to 03. Note that. parameter 73 does not transpose pitch. It controls the root for the scale selected by parameter 74. Note that parameter 73 has no effect on an equal tempered scale. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pythagorean | |||||||||||
| 261.6 | 279.4 | 294.3 | 310.1 | 331.1 | 348.8 | 372.5 | 392.4 | 419.1 | 441.5 | 465.1 | 496.7 |
| Van Zwolle | |||||||||||
| 261.6 | 279.4 | 294.3 | 314.3 | 331.1 | 353.6 | 372.5 | 392.4 | 419.1 | 441.5 | 471.5 | 496.7 |
| Meantone | |||||||||||
| 261.6 | 272.8 | 292.3 | 313.2 | 326.7 | 350.0 | 365.0 | 391.1 | 407.9 | 437.0 | 468.3 | 488.3 |
| Silbermann I | |||||||||||
| 261.6 | 275.0 | 293.0 | 312.2 | 328.1 | 349.6 | 367.5 | 391.6 | 411.6 | 438.5 | 467.2 | 491.1 |
| Silbermann II | |||||||||||
| 261.6 | 276.2 | 293.0 | 312.2 | 329.6 | 349.6 | 369.2 | 391.6 | 413.4 | 438.5 | 467.2 | 493.3 |
| Rameau | |||||||||||
| 261.6 | 276.9 | 293.3 | 309.7 | 330.4 | 348.8 | 369.2 | 391.1 | 413.9 | 438.5 | 463.0 | 493.9 |
| Werckmeister III | |||||||||||
| 261.6 | 277.5 | 293.3 | 311.1 | 328.9 | 350.0 | 370.0 | 391.1 | 414.8 | 438.5 | 466.7 | 493.3 |
| Werckmeister IV | |||||||||||
| 261.6 | 275.6 | 293.0 | 311.5 | 329.6 | 348.8 | 369.2 | 390.7 | 413.4 | 437.5 | 467.2 | 492.2 |
| Werckmeister V | |||||||||||
| 261.6 | 275.6 | 293.3 | 311.1 | 328.9 | 348.8 | 368.7 | 392.4 | 413.4 | 438.5 | 465.1 | 493.3 |
| Werckmeister VI | |||||||||||
| 261.6 | 278.3 | 293.8 | 311.3 | 331.1 | 349.5 | 372.5 | 391.7 | 414.2 | 441.5 | 466.9 | 496.7 |
| Kirnberger II | |||||||||||
| 261.6 | 277.5 | 294.3 | 312.2 | 328.9 | 348.8 | 370.0 | 392.4 | 416.2 | 438.5 | 465.1 | 493.3 |
| Kirnberger III | |||||||||||
| 261.6 | 277.5 | 293.3 | 311.1 | 328.9 | 348.8 | 370.0 | 391.1 | 414.8 | 438.5 | 465.1 | 493.3 |
| Italian 18th Century | |||||||||||
| 261.6 | 277.2 | 293.0 | 311.1 | 328.9 | 349.2 | 370.0 | 391.1 | 414.4 | 438.0 | 465.1 | 492.8 |
| Equal Temperament | |||||||||||
| 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 |
Dating back to 500 BC, this simple scale creates eleven pure fifths around the circle, leaving the entire Comma between G# and Eb There are four pure major thirds at B-D#, F#-A#, Db-F, and Ab-C, but these are not particularly useful. The remainder are quite harsh.
Arnout Van Zwolle (1400-1466) modified the Pythagorean scale by placing the Comma between B and F#. This moved the thirds to D-F#, A-C#, E-G#, and B-Eb, which were more useful. This gives pure major triads on D, A and E.
The best known of the old scales, this scale emphasizes pure thirds by making the fifths narrow. It was certainly in use by the end of the 15th century, if not earlier. It has the greatest number of pure triads of any of the scales on this disk. All whole steps are equally spaced, one half of a major third apart. It also has a very prominent "wolf" between G# and Eb- If the circle is extended down to Ab, the pitch is very different from the G#, Some baroque keyboards had a split pair of black keys that allowed the musician to choose G# or Ab.
Organ builder Gottfried Silbermann (1678-1734) tried several variants to narrow the "wolf" and make his instruments useable in more keys. None of the intervals of these two scales are pure.
Jean Phillipe Rameau. (1683-1764) modified the meantone scale to provide three pure fifths. This very pleasant scale almost completely eliminates the harsh "wolf" of the meantone while preserving most of its pure harmony.
Organ builder and mathematician Andreas Werkmeister (1645-1706) devoted much of his life to the study of temperament and suggested many. different scales. The best known of these are included on this disk. His goal was to place the best thirds in those keys with the fewest incidentals. It is very likely that Bach (l685-1750) wrote his famous "Well-tempered Klavier" pieces for one of these temperaments.
Composer and music theorist Johann Philipp Kirnberger (1721-1783) suggested several temperaments. The two scales here offer a large number of pure fifths. The first has pure thirds at C-E, G-B, and D-F# but the fifths at D-A and A-E are somewhat harsh. Kirnberger later proposed an alternate scale with smoother fifths, but only one pure third at C-E.
One of the many variations commonly in use in the 18th century that emphasized a pure third at C-E and distributed the "wolf" around the circle of fifths. There is only one pure interval in this scale.
This scale is supplied for fun and has no significant historical precedent. When used to play well known sequences it offers some insight into the concept of the inverted interval.
This scale is so common in the 20th century that many musicians and instrument makers don't know that there are any alternatives. Dividing the Pythagorean Comma equally around the circle of fifths is not a recent idea. Equal temperament was probably known in the 1700s or earlier, but was not considered a satisfactory scale due to the impurity of all intervals. In the late 18th and 19th centuries, composers increasingly explored modulation to many different keys. They found that most temperaments were unsatisfactory because of the significant tonal changes involved in changing keys. The equal-tempered scale was begrudgingly recognized as an acceptable compromise that worked equally in all keys. It is only through over a century of dominance that this scale has become the one that we are accustomed to - the scale that sounds "in tune" to us today.
The principal source of information used to create these temperaments is HARPSICHORD TUNING - A COURSE OUTLINE, by G.C. Klop, distributed by The Sunbury Press, P.O. Box 1778, Raleigh, NC 27602.